改写 7 年前的 Perl 程序,记录一些优化的思路
这周心血来潮帮别的 lab 做点分析的工作,顺便学了下算法。结果发现原来的 Perl 程序跑起来很慢,于是就想着能不能改写成 Python 程序,然后再优化一下。
算法原理
在 DamID-seq 或者 ChIP-seq 等技术中,由于本质上记录的是一种“亲和力”,因此数据中会包含很多非特异性亲和的噪声数据。所以如果我们需要一种算法来找到特异性亲和的峰,避免将由概率产生的噪声数据误认为是特异性亲和的峰。
find_peaks 算法的实现思路其实很简单,大体来讲分成以下几步:
- 读入数据:damidseq_pipeline 会将原始的测序结果比对到参考基因组上,在后续处理中又会生成一个
score来反应亲和力。每条记录还包括了chr、start、end等信息,分别对应基因组、比对的起始与结束位置。 - 计算百分位:将结果中非空的
score进行排序,然后计算出指定的百分位对应的score值。(由百分位起点min_quant和步长step决定) - 计算出现概率:将记录打乱后,根据上述步骤得到的
score各个百分位阈值进行筛选,如果连续遇到min_count以上条记录的话则认为其为一个峰。重复N次,累积记录下每个阈值对应的能找到的峰的大小和数量。 - 线性回归:对于上面这样的随机排列后的计算,我们可以认为在每个超过阈值的值是均匀分布在整个数据集中的。因此每个这样的值之后再出现一个同样满足条件的值的概率应该是固定的,如果记 $m$ 长的峰观测到数量的平均值为 $\mathbf{F}(m)$,那么应有 $\mathbf{F}(m+1)\approx\mathbf{F}(m)\cdot P$,这里的 $P$ 为常数,反应了阈值之上的值分布的密度。因此观测到的峰的数量和大小之间应该是一个指数分布的关系,故我们对观测数量取对数后可以拟合得到一个线性关系。
- 统计真实出现频数:和 (3) 步类似,只不过这里我们不打乱记录的顺序,并且遵循其对应的染色体归属和先后顺序,统计各个阈值对应出现的峰的大小与数量的关系。
- 计算假阳性率(False Discovery Rate, FDR):上述得到的拟合关系为每个百分位阈值对应一个,运用这个结果,我们可以预测出每个阈值下观测到的特定大小的峰在纯随机分布中出现的数量,将其与真实观察到的数量做比,则可得到该阈值下观测到该长的峰的假阳性率。通过控制
FDR,则可以得到各个阈值条件下识别为显著峰所需的最小长度。 - 计算显著峰:根据上一步的计算结果,筛选出那些显著的峰。
- 合并显著峰:将同一个染色体内的显著峰进行合并(通常是由不同阈值下均显著而产生的重复结果),并且得到重叠峰的最大
score和最小FDR,将结果写入文件中。
复刻算法
有了以上的思路之后,我们写程序就很快了。为了能让程序能够以尽量少的依赖跑起来,因此我们只使用 Python 内置的库来实现所有功能。写完这版后,我用较小的 N 测试了 Perl 程序和 Python 程序的效率,结果大致如下:
| $N=10$ | Perl | Python |
|---|---|---|
| 耗时 (秒) | 240s | ~ 210s |
优化算法
既然提升不明显,那我们肯定是不满意的,拿神奇的 scalene 跑一下分析,发现耗时很多是花在判断 score 是否为 $0$ 上面了。这个部分原先的逻辑我是照搬的 Perl 程序,因此对于每一条记录,不管是在计算百分位阈值还是计算统计出现频次的时候,都需要首先判断其 score 是否为 $0$,如果是的话,那么就忽略这条记录。
因此尝试一下用 Python 内置的 filter 函数来对结果进行过滤,这样就不需要使用 if 分支进行判断了(内置的实现一般来讲会快一些):
@ def call_peaks_unified_redux
~ ...
- total = len(probes)
- for i in range(total):
- chrom, start, end, score = probes[i]
- if not score:
- continue
+ for chrom, start, end, score in filter(lambda x: x[3], probes):
~ ...再测试一下,效果不错,速度提升很明显
| $N=10$ | Perl | Python |
|---|---|---|
| 耗时 (秒) | 240s | ~90s |
但是!我还是不满意,这跑一下还是得一分多钟,更何况这还是缩小了迭代次数的条件下测试的,在实际使用中,越大的 N 才能够保证随机出来的结果覆盖尽可能多的可能,因此线性拟合的结果才会更准确,所以我们可以再想想哪里可以优化。
仔细分析代码我们可以发现:
load_gff:加载文件时score为0或NA的记录也会存入结果数组中find_quant:遇到score为0记录时,会跳过这条记录,对结果不影响find_randomised_peaks:随机打乱记录时,如果指定了只取部分的记录,则有可能取到score为0的记录call_peaks_unified_redux:遇到score为0记录时,会跳过这条记录,对结果不影响
因此也就是说,读入的数据中,score 为 0 的记录占了大部分,而我们在计算的时候,却不需要考虑这些记录。这些记录唯一影响的就是 find_randomised_peaks 取子集的情况,因此如果我们能够处理好这个部分的逻辑,我们就可以在读入时就过滤掉这些记录,从而减少后续的计算量。
首先改写一下 load_gff 函数,直接忽略那些空的记录,同时为了保证计算出来的覆盖率等等保持不变,我们将后续函数的逻辑提到此处:
@ def load_gff
+ total_coverage = 0
~ ...
~ for line in lines:
~ ...
+ # increment raw reads number
+ RAW_READS_NUM += 1
+ # skip empty reads
+ if score == "NA" or not float(score):
+ continue
+ # record read
~ parsed_result.append(
~ (
~ CHROM(chrom),
~ START(POS(int(start))),
~ END(POS(int(end))),
- SCORE(float(score) if score != "NA" else 0),
+ SCORE(float(score)),
~ )
~ )
+ # record total coverage
+ total_coverage += int(end) - int(start)
~ ...
+ sys.stderr.write(f"Total coverage was {total_coverage} bp\n")然后在 find_quant 函数中,我们就不需要做额外的判断了:
@ def find_quant
~ ...
- total_coverage = 0
- frags: list[SCORE] = list()
- for (chrom, start, end, score) in filter(lambda x: x[3], probes):
- total_coverage += end - start
- frags.append(score)
+ frags = [x[3] for x in probes]
~ frags = sorted(frags)
- sys.stderr.write(f"Total coverage was {total_coverage} bp\n")
~ ...对于 call_peaks_unified_redux 也是同理:
@ def call_peaks_unified_redux
~ ...
~ for pm in peakmins:
~ ...
- for chrom, start, end, score in filter(lambda x: x[3], probes):
+ for chrom, start, end, score in probes:
~ ...对于 find_randomised_peaks 则稍微麻烦一些,不过我们还是能做得不比原程序差的。在原程序中,如果指定了 frac,则只采用固定的前 frac 条记录用于估计期望频率(此处 frac 为整数),因此很有可能遇到前 frac 条记录中为空的占比大于或小于空记录占总记录条数的比例,而且一旦出现这种情况则意味着这种偏差会出现在每次打乱记录的结果中。因此这里我们改用一种更普适的做法:
- 令
frac为 $r\in(0,1]$ 区间内的浮点数,代表我们需要取的记录的比例 - 在生成数据集时,模拟从总 $M$ 条记录中取 $\left\lfloor r\cdot M\right\rfloor$ 条,计算出其中非空的记录数 $K$
- 以 $K$ 为采样量来从非空的记录中采样,得到的子集用于估计期望
@ def find_randomised_peaks
~ ...
~ for iter_num in range(args.n):
~ ...
+ # This is a naive approximation to randomly sample a fraction
+ # as the full sequence doesn't contain empty reads
+ # (but no worse than the original approach anyway)
~ if args.frac:
- pbs = pbs[: args.frac]
+ num_to_sample = sum(
+ map(
+ lambda x: x <= int(RAW_READS_NUM * args.frac),
+ random.sample(range(RAW_READS_NUM), int(RAW_READS_NUM * args.frac)),
+ )
+ )
+ pbs = random.sample(probes, num_to_sample)
~ ...其他一些地方也做了一些小的调整来对应以上改动,但是这些改动都是比较简单的,因此就不一一列举了。
我们再次测试一下,结果非常的 amazing 啊!
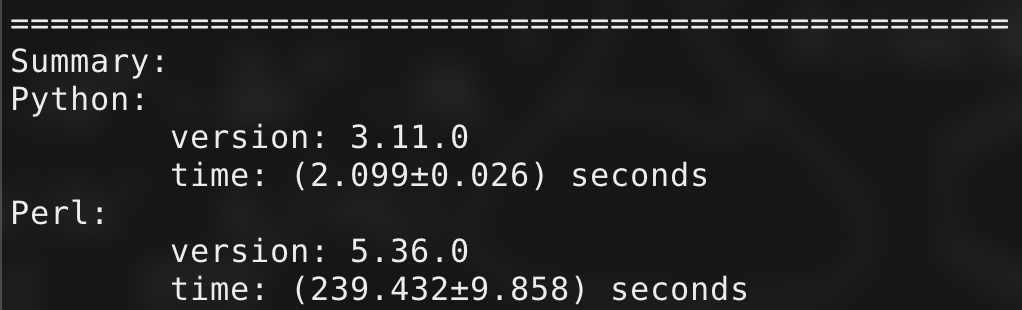
如果使用默认的参数来跑(N: $100$, fdr: $0.01$, min_count: $2$, min_quant: $0.95$, step: $0.01$),原来的 Perl 程序需要约 $40$ 分钟,而现在的 Python 程序只需要十几秒,直观感受就是:

感知很强!代码均已遵循 GPLv3 协议开源,仓库链接。
